Probabilistic Collision and Grounding Analysis
Fujii and MacDuff (1974)
Already in 1974 Fujii et al. [5] and also MacDuff [21] initiated more systematic and risk based approaches for grounding and collision analysis. MacDuff studied grounding and collision accidents in the Dover Strait and calculated a theoretical probability of the both the grounding and the collision event. This probability was calculated by assuming all vessels to be randomly distributed in the navigational channel.
Geometric Probability
MacDuff denoted the thus obtained probability the geometric probability, since this probability was entirely based on a geometric distribution of ships that were “navigating blind”. By comparing to the observed number of grounding and collision it was found that the geometric probability predicted too many events and a correction factor Pc was introduced to account for the difference.
Causation Probability
The correction factor was denoted the Causation Probability and it models the vessels and the officer of the watch’s ability to perform evasive manoeuvres in the event of potential critical situation.
In the study MacDuff found that the causation probability was 10-4 for collisions in crossings, and 5⋅10-4 for head-on collisions. Using an approach similar to MacDuff [21], Fujii et al. [5] introduced a probability of mismanoeuvres on the basis of grounding statistics for several Japanese straits. For the considered straits the probability was found to be in the range from 0.6⋅10-4 to 1⋅10-3.
Common for both studies is that they assume the vessels to be randomly distributed over the considered waterway.
It is in this respect very important to note that the causation probability obtained in the two studies is dependent on this (rather crude) assumption. Hence, in case a more realistic distribution of the ship traffic over the waterway is assumed, then the causation probability will change accordingly.
The advantage of the approach suggested by Fujii et al. [5] and by MacDuff [21] is its simplicity and the related robustness. This is, however, also a drawback since the defined causation probabilities cannot be directly used if more detailed models are applied for the geometrical distribution of the vessels. Nonetheless, the two studies provide a proper framework for the general risk model for evaluating the frequency of grounding and collision accidents, and they provide valuable guidelines for the order of magnitude of the causation probability.
Risk models
Today most risk models for estimating the grounding or collision frequency are rooted in the approach defined by Fujii et al. [5] and by MacDuff [21]. That is, the potential number of ship grounding or ship-ship collisions is first determined as if no aversive manoeuvres are made.
This potential number of ship accidents is based on 1) an assumed or prespecified geometric distribution of the ship traffic over the waterway and 2) on the assumption that the vessels are navigating blindly as these are operating at the considered waterway. The thus obtained number of potential accident candidates (often called the geometric number of collision candidates) is then multiplied by a specified causation probability to find the actual number of accidents. The causation probability, which acts as a thinning probability on the accident candidates, is estimated conditional on the defined blind navigation.
The above-described approach is often termed the scenario approach, since it utilises certain accident scenarios and statistics for the cause of these scenarios. The statistics mainly come into the analysis through the defined value of the causation probability. This implies that the scenario approach as applied today – in principle – represents all types of accident scenarios, provided that they are included in the statistical basis.
An alternative risk analytical approach, the synthesis approach, see Gluver and Olsen [12], base the risk of grounding or collision on a set of scenarios where specific error situations or conditions are assumed to occur or exist in the vessel prior to or during the considered critical situation. Such an approach, however, requires that all significant accident scenarios are identified and analysed. Consequently, this also implies that the causation probability must be defined conditional on considered accident scenario. It therefore follows that the advantage of introducing the synthesis approach is that alternate risk-mitigating aspects more easily may be both identified and quantified.
Examples of different accident scenarios could be rudder stuck, power failure, navigational error, etc. Each of these scenarios may be further sub-divided to describe the scenario in more details e.g., in what position the rudder is stuck and what other equipment is available to mitigate the problem.
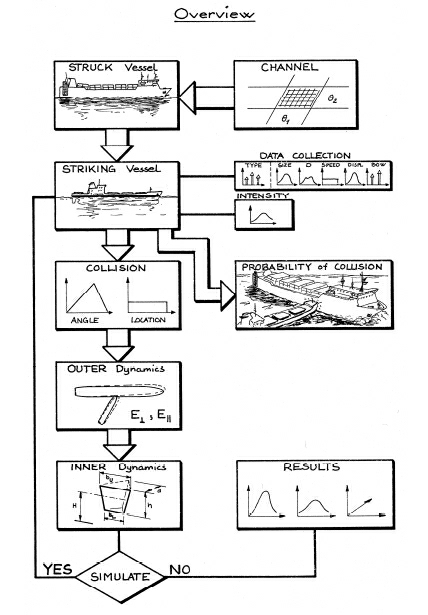
Figure 1 Process for probabilistic prediction and spatial distribution of collision damages.
In the present work the scenario approach is applied and the procedure is schematically illustrated in Figure 1 for the collision analysis. A grounding analysis follows the same conceptual outline.
Basically the procedure is as follows:
- First the relevant navigational area is described. This involves description of the traffic composition along all navigational routes and descriptions of all grounds in the vicinity of the route.
- Next the considered vessel (termed struck vessel in Figure 1) is defined to be operating on a specified route in the defined navigational area. All potential other vessels (striking vessel in Figure 1) or grounds is then identified and the probability of grounding and collision is calculated.
- Subsequently, the identified ground or striking vessel may further be used for calculating damage statistics.
The ensuing consequence analysis (in terms of time to capsize, oil outflow, etc.) of the identified damages is not shown in the figure, but statistics for this may similarly be obtained.
Although the procedure described above resembles the scenario approach the alternative synthesis approach may also be covered by careful application of the causation factors.
Calculating Collision Frequencies
Based on the mathematical models for estimating the collision and grounding frequencies described on this site, a computer program has been written (IWRAP) for calculation of grounding and collision frequencies in specific waterways where the waterway layout, traffic volume and composition as well as the ship traffic lateral distribution are known.
The idea behind the procedure is that vessels are operating on specific route. The traffic routes are built of a series of waypoints that are connected by legs. On each leg the number of vessels as a function of size and type and their overall spreading are defined. Each leg may be connected to zero, one or more other segments at its end points.
In principle three different types of collisions can occur.
Head-On or Overtaking Collision
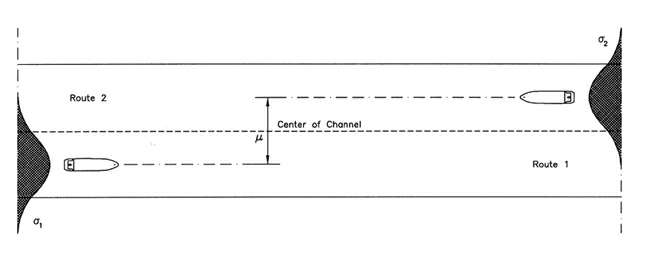
One type of collision is head-on induced collisions due to two way traffic in the straight waterway segments or overtaking taking collisions as shown in Figure 2.
Figure 2, Head-On or Overtaking Collision Scenario
Bend Collision
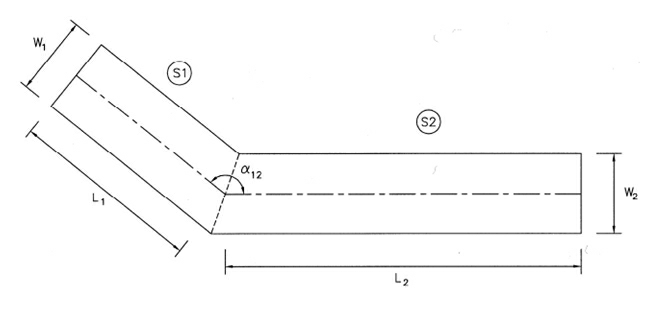
Another type of collision occurs at bends where only two straight route segments intersect, see Figure 12. At such an intersection a ship can become a collision candidate if the course is not changed at the intersection. This probability of omission P0 is taken as 0.01.
Figure 12 Bend Collision Scenario at the intersection between two straight waterway segments.
Crossing or Merging Collision
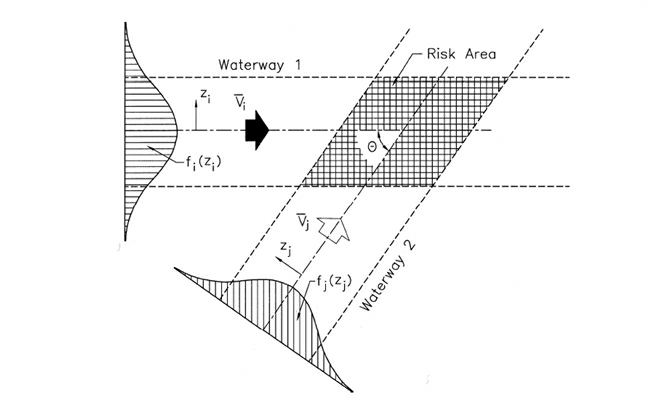
Finally, when more than two legs meet at a waypoint the model calculates the probability for crossing collisions, as indicated in Figure 3. Dependent on how the vessel traffic on the legs meets each other, the scenario will be characterized either as either a crossing collision, a merging collision, or a bend collision.
Figure 3 Crossing or Merging Collision Scenario
Causation Factors
For each leg the identified number of collision candidates related to head-on, bends, and crossings is calculated for each vessel type and is subsequent multiplied by a causation factor. The following causation factors inspired by Fujii et al. [8] are used:
| P[head-on] | = 0.5 ∙ 10-4 |
| P[bend] | = 1.3 ∙ 10-4 |
| P[crossing] | = 1.3 ∙ 10-4 |
These values for the causation factor are typical values for well regulated ship traffic in Japan. The causation factor will be a function of visibility, darkness, current and wind in the actual geographical area. All these factors suggest that larger values should be used around the Nordic countries.
However, Fujii has also observed that passenger ferries have smaller collision probabilities than ordinary merchant vessels. This is due to the navigator awareness of the area and the fact that there are two navigator onboard passenger ferries.
Combined causation factor Pci,j
The causation probability, Pci,j , represents the probability that for example none of the (two) officers on watch on the two vessels manage to react in time and avoid the collision. This implies that the conditions present on both vessels are of importance in the determination of the magnitude of the causation joint factor.
Different conditions may be present that lead to higher (or lower) safety standards compared to the average ship. This could for instance be the presence of a pilot, improved bridge layout and navigational equipment, or the presence of two navigators as is the case on most passenger ferries. The presence of such safety increasing conditions will imply that the joint causation factor, Pci,j ,for the two vessels will decrease.
In the study “Oil and Chemical Spills is Danish waters” it was proposed to compile the joint causation factor as:
This is a justifiable pragmatic approach that assures a balance between failures of the navigational watch keeping on the two vessels.
|
Source: IWRAP Mk II, Basic Modelling Principles for Prediction of Collision and Grounding Frequencies, (draft working document), Rev. 4, 2008.03.09, Peter Friis-Hansen, Technical University of Denmark. |